As everyone learns in grade school, typical 1-dimensional cellular automata are identified at the edges and thus their evolutions form topological cylinders. An obvious method of visualization then is a proper geometric cylinder:
-
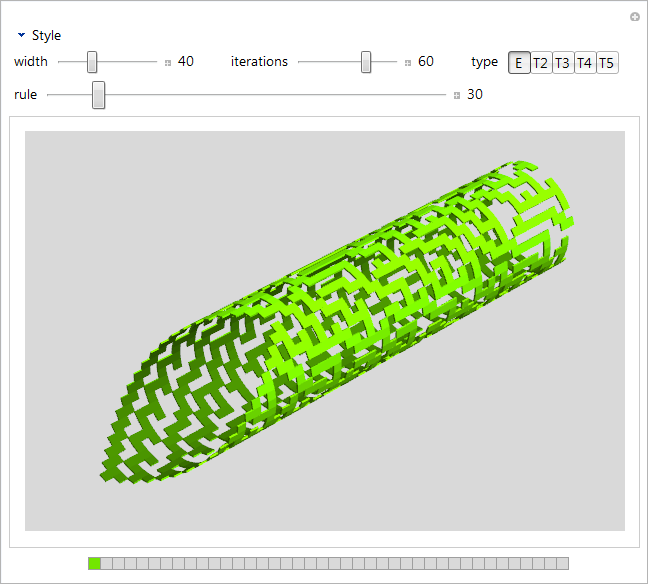
-
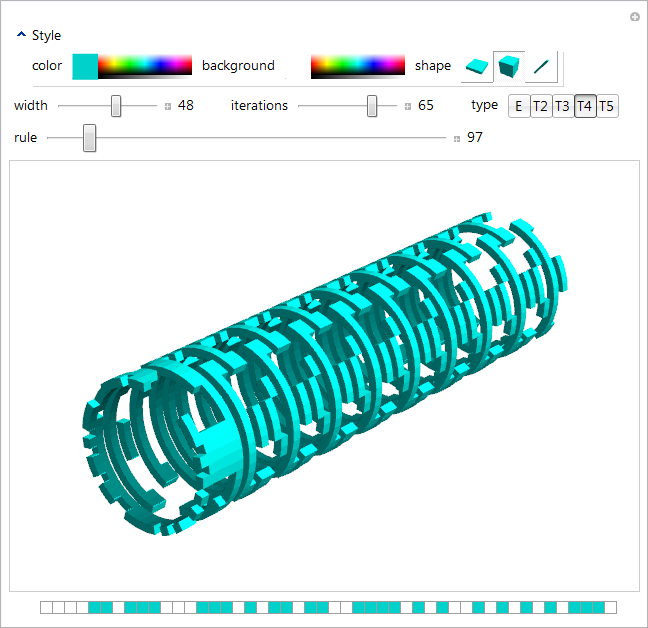
-
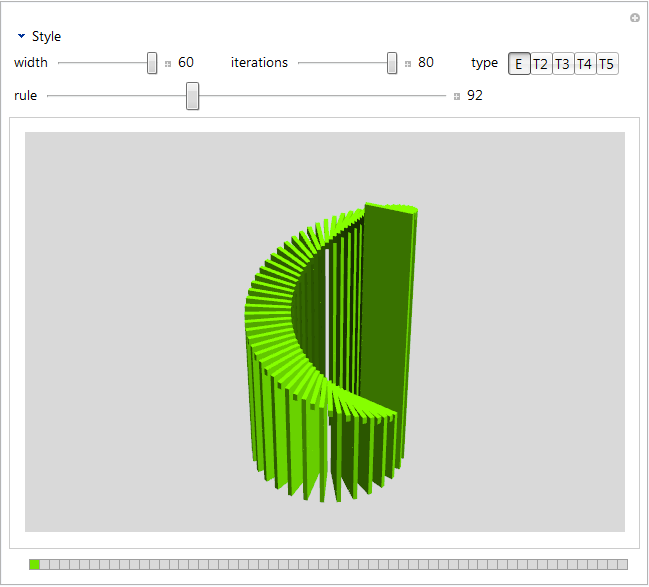
-
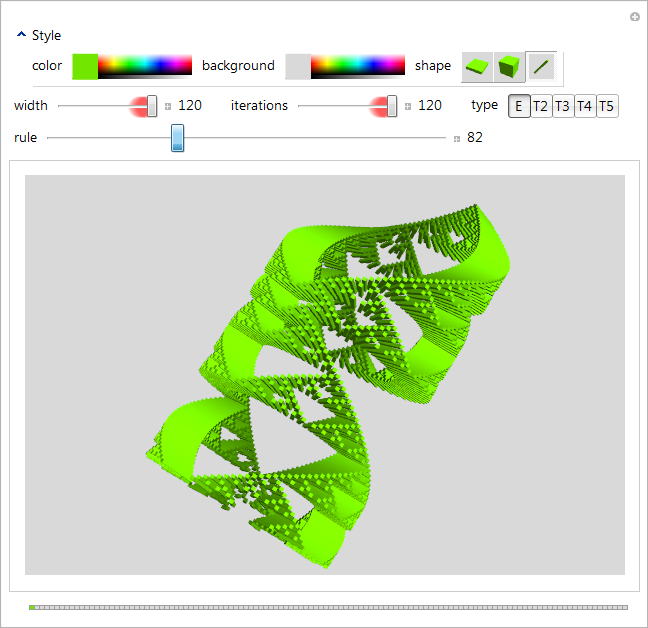
-
-
graphicsSize = {600, 400}; gridControlHeight = 14; shapeChoicesIconSize = {25, 25}; {widthDefault, widthMin, widthMax} = {40, 30, 60}; {iterationsDefault, iterationsMin, iterationsMax} = {60, 10, 80}; (*shape choices*) createShapeChoices[ls_] := Module[{}, (shapeOverlap[#[[1]]] = #[[4]]) & /@ ls; #[[1]] -> Tooltip[Graphics3D[{EdgeForm[], Dynamic[color], Rotate[Cuboid[{0, 0, 0}, {1, 1, #[[1]]}], #[[3]], {0, 1, 0}]}, Background -> Dynamic[background], Lighting -> "Neutral", Boxed -> False, ImageSize -> shapeChoicesIconSize], #[[2]], TooltipDelay -> .3] & /@ ls]; shapeChoices = createShapeChoices[{{.2, "wafer", 0, 0}, {1, "block", 0, .14}, {12, "spaghetti", \[Pi]/5, .14}}]; (*CellularAutomaton choices and the range of the 'rule' slider*) automata = { {{n, 2, 1}, " E ", "Elementary", 255}, {{n, {2, 1}, 2}, "T2", "Totalistic, Range 2", 63}, {{n, {2, 1}, 3}, "T3", "Totalistic, Range 3", 255}, {{n, {2, 1}, 4}, "T4", "Totalistic, Range 4", 1023}, {{n, {2, 1}, 5}, "T5", "Totalistic, Range 5", 4095}}; typeChoices = #[[1]] -> Tooltip[#[[2]], #[[3]], TooltipDelay -> .1] & /@ automata; Do[ruleMax[a[[1]]] = a[[4]], {a, automata}]; (*initial array operations*) opList = { (*reset*) Grid[List@{Dynamic[ ArrayPlot[{Table[If[i == 1, 1, 0], {i, 1, 9}]}, Mesh -> All, ColorFunction -> arrayColor, ColorFunctionScaling -> False], TrackedSymbols :> {arrayColor}], "reset"}, Alignment -> {Center, Center}] :> (initialArray = ConstantArray[0, width]; initialArray[[1]] = 1), (*invert*) Grid[List@{Dynamic[ ArrayPlot[{Table[If[i == 1, 0, 1], {i, 1, 9}]}, Mesh -> All, ColorFunction -> arrayColor, ColorFunctionScaling -> False], TrackedSymbols :> {arrayColor}], "invert"}, Alignment -> {Center, Center}] :> (initialArray = Boole[# == 0] & /@ initialArray), (*randomize*)Module[{conjure, entropyList}, conjure[] := While[Entropy[entropyList = RandomInteger[{0, 1}, 9]] < .65]; conjure[]; Grid[List@{Dynamic[ArrayPlot[{entropyList}, Mesh -> All, ColorFunction -> arrayColor, ColorFunctionScaling -> False], TrackedSymbols :> {arrayColor, entropyList}], "randomize"}, Alignment -> {Center, Center}] :> (initialArray = RandomInteger[{0, 1}, width]; conjure[])]}; (*color scheme bookmarks*) ColorSchemeIcon[foreground_, background_] := Graphics[{background, Rectangle[{0, 0}, {1, 1}], foreground, Rectangle[{.25, .25}, {.75, .75}]}, ImageSize -> {20, 20}] ColorSchemeIcon[foreground_, background_, True] := Graphics[{ foreground, Rectangle[{0, 0}, {.5, 1}], background, Rectangle[{.25, .25}, {.5, .75}], background, Rectangle[{.5, 0}, {1, 1}], foreground, Rectangle[{.5, .25}, {.75, .75}]}, ImageSize -> {20, 20}]; colorSchemes = { {Darker[Blend[{Yellow, Green}], .1], Lighter[Gray, .7], "default"}, {invert, "invert colors"}, {RGBColor[1, .9495, .125], RGBColor[0, .5384, .04806]}, {RGBColor[1, .3846, .7143], Lighter[Gray, .9]}, {RGBColor[.577, .1539, 1], RGBColor[.0879, 0, .3077]}, {RGBColor[0, .8182, .7918], White}, {White, Black}}; colorSchemeList = (# /. { {invert, t_} :> (Grid[ List@{Dynamic@ColorSchemeIcon[background, color, True], t}, Spacings -> .5, Alignment -> {Center, Center}] :> With[{swap = color}, {color = background, background = swap}]), {f_, b_} :> (Grid[List@{ColorSchemeIcon[f, b]}, Spacings -> .5, Alignment -> {Center, Center}] :> {color = f, background = b}), {f_, b_, t_} :> (Grid[List@{ColorSchemeIcon[f, b], t}, Spacings -> .5, Alignment -> {Center, Center}] :> {color = f, background = b}) }) & /@ colorSchemes; fullRandomBookmark = Grid[{{"Full Random"}}] :> Module[{}, color = RGBColor[RandomReal[{0, 1}, 3]]; background = RGBColor[RandomReal[{0, 1}, 3]]; thickness = RandomChoice[{.5, .3, .2} -> shapeChoices][[1]]; width = RandomInteger[{widthMin, widthMax}]; iterations = RandomInteger[{iterationsMin, iterationsMax}]; type = RandomChoice[typeChoices][[1]]; rule = RandomInteger[{0, ruleMax[type]}]; initialArray = RandomInteger[{0, 1}, width]]; (*the control used for adjusting the initial array*) gridControl[Dynamic[var_], colorFunction_, maxWidth_, height_] := DynamicModule[{lastValue, lastIndex = -1, mouseLoc}, mouseLoc[] := Module[{pos = MousePosition["Graphics"]}, If[pos === None, None, Ceiling[Abs[First@pos]]]]; (*main gridControl output*) Panel[#, ImageSize -> maxWidth, Alignment -> Center, Appearance -> "Frameless", FrameMargins -> 0] &@ EventHandler[ Dynamic[ArrayPlot[{var}, Mesh -> All, ImageSize -> {{maxWidth}, height}, ColorFunction -> colorFunction, ColorFunctionScaling -> False, PlotRangePadding -> 0]], {"MouseDown" :> Module[{x = Clip[mouseLoc[], {1, Length[var]}]}, If[Head[x] =!= Integer, Return[]]; var[[x]] = Boole[var[[x]] == 0]; lastValue = var[[x]]], "MouseDragged" :> Module[{x = Clip[mouseLoc[], {1, Length[var]}]}, If[Head[x] =!= Integer, Return[]]; If[x =!= lastIndex,(*only when entering new cell*) lastIndex = x; var[[x]] = lastValue]]}]]; (*function that creates the Cuboids*) render[stack_, iterations_, color_, thickness_, overlap_] := Module[{ center, interval, width = Length[stack[[1]]]}, interval = 2. \[Pi]/width; Last@Reap[Do[ Sow[Rotate[ Last@Reap[Do[ If[stack[[level, rad]] == 1, center = {Cos[interval*rad]/interval, Sin[interval*rad]/interval, 0} // N; Sow[Cuboid[center + {0, 0, -level} + {thickness, overlap/2 + .52, .52}, center + {0, 0, -level} - {0, overlap/2 + .52, .52}], color]; (*make the cylinder darker on the inside*)Sow[Cuboid[ center + {0, 0, -level} + {0, overlap/2 + .52, .52}, center + {0, 0, -level} - {.02, overlap/2 + .52, .52}], Darker[color, .5]]], {level, 1, iterations}], _, {#1, #2} &], interval*rad, {0, 0, 1}, center]] , {rad, 1, width}]]]; (*Manipulate*) Manipulate[Module[{stack}, (*mention these so that they are saved in CDF*) {opList, colorSchemeList, fullRandomBookmark}; (*clamp 'rule' slider max*) If[rule > ruleMax[type], rule = ruleMax[type]]; (*readjust length of initial array*) If[Length[initialArray] != width, initialArray = PadRight[initialArray, width]]; (*the 2D matrix*) stack = CellularAutomaton[type /. n -> rule, initialArray, iterations]; (*prevent recursive updating*) If[arrayColor[0] =!= background || arrayColor[1] =!= color, arrayColor[0] = background; arrayColor[1] = color]; (*main output. this Overlay/ControlActive structure is to prevent the user's adjustments to the Graphics3D pane from being lost, as they would be with a simple ControlActive[a,b] setup*) Overlay[{ Graphics3D[{EdgeForm[], ControlActive[Null, If[Total@Total@stack > 0, a = render[stack, iterations + 1, color, thickness, shapeOverlap[thickness]]]]}, Lighting -> "Neutral", Background -> background, Boxed -> False, ImageSize -> graphicsSize], ControlActive[ArrayPlot[stack // Transpose, ColorFunction -> arrayColor, ColorFunctionScaling -> False, Frame -> False, ImageSize -> graphicsSize], ""]}, All, 1, Alignment -> Center] (*endModule*)] (*Manipulate options*) , OpenerView[{"Style", Grid[List@{ Control@{color, Darker[Blend[{Yellow, Green}], .1], ImageSize -> Small, ContinuousAction -> False}, Control@{background, Lighter[Gray, .7], ImageSize -> Small, ContinuousAction -> False}, Control@{{thickness, .2, "shape"}, shapeChoices, ControlType -> SetterBar, Background -> background}}, Dividers -> {{False, False, False, True}, {False, True}}, FrameStyle -> Directive[Opacity[.5], Darker@Gray]]}], Grid[List@{ Control@{{width, widthDefault}, widthMin, widthMax, 1, Appearance -> "Labeled", ImageSize -> Small}, Control@{{iterations, iterationsDefault}, iterationsMin, iterationsMax, 1, Appearance -> "Labeled", ImageSize -> Small}, Control@{{type, typeChoices[[1, 1]]}, typeChoices, ControlType -> SetterBar}}, Spacings -> 0], {{rule, 30}, 0, ruleMax[type], 1, Appearance -> "Labeled", ImageSize -> Large}, {{initialArray, {1}, Null}, gridControl[#1, arrayColor, graphicsSize[[1]], gridControlHeight] &, ControlPlacement -> Bottom}, Alignment -> Center, AppearanceElements -> "ManipulateMenu", SaveDefinitions -> True, Bookmarks :> { Sequence @@ opList, Sequence @@ colorSchemeList, fullRandomBookmark} (*endManipulate*)]
The awesomeness of this program is acceptable, I suppose. However I wrote it when I was just starting to get the hang of Mathematica. For a more idiomatic approach to the geometry (one using Position), see my more recent cellular automata 3D 1. And for a more methodical approach to structuring larger programs of this kind, see my matrix replacement 2.
