L-systems are simple rule-based constructions that can make pretty fractals. Ergo the obligatory Mathematica program:
-
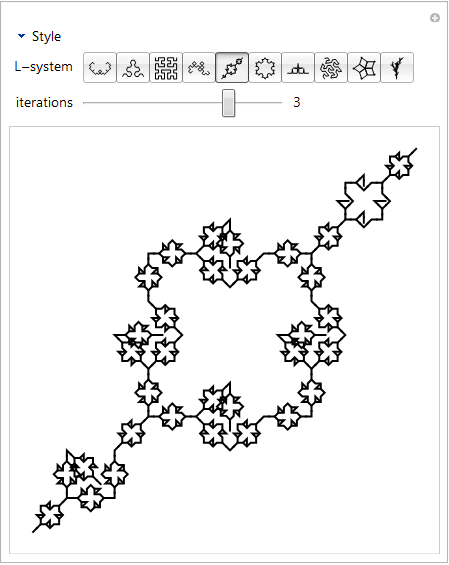
-
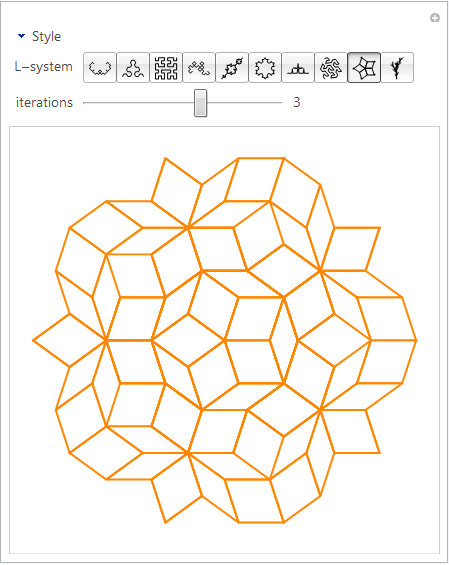
-
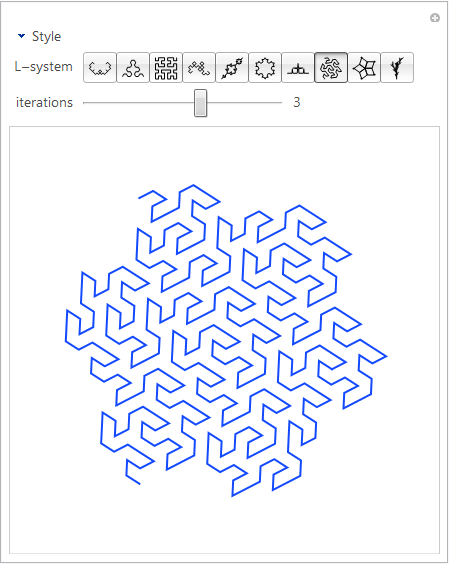
-
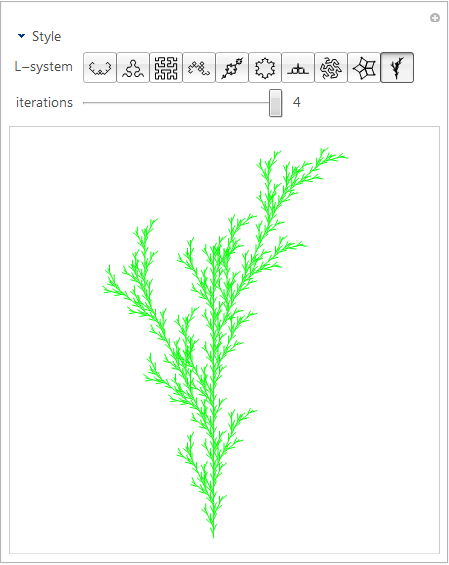
-
imageSize = {400, 400}; thumbSize = {26, 26}; thumbPadding = 2; nextStyle = {RGBColor[1, .6, .6], Dashing[1 / (40 + 3^(i+1))]}; maxIterations = 5; (* initialized so it's not Null *) (* ignore these warnings *) Off[Part::partw]; Off[Rule::rhs]; Off[Join::heads]; (* main LSystem function. it does ReplaceAll in a way that splices into the list *) Module[{adjustment = { Rule[a_, b_] :> Rule[a, Sequence @@ b], RuleDelayed[a_, b_] :> RuleDelayed[a, Sequence @@ b]}}, LSystem[0, axiom_, _] := axiom; LSystem[iterations_, axiom_, rule_] := LSystem[iterations - 1, axiom, rule] /. (rule /. adjustment); ]; (* main drawing function. executes a sequence of movement commands *) LOGO[commands_, {startx_, starty_, starta_}] := Block[{ (* note that these commands are functions *which construct* transformations that operate on the turtle's state *) forward = {x_Real, y_Real, a_Real} -> {x + # Cos[a], y + # Sin[a], a} &, left = {x_Real, y_Real, a_Real} -> {x, y, a + # Degree} &, backward = forward[-#] &, right = left[-#] &, push, pop}, (* LIFO stack *) {push, pop} = Module[{list = {}}, {triple_ :> (AppendTo[list, triple]; triple), _ :> Module[ {val = list[[-1]]}, list = Delete[list,-1]; val]}]; Block[{ (* remove non-commands *) filteredCommands := filteredCommands = Cases[commands, _Rule | _RuleDelayed], (* split lines where there is a pop command *) spans := spans = Join[{0}, Position[filteredCommands, pop] // Flatten, If[filteredCommands[[-1]] =!= pop, {Length[filteredCommands]+1}, {}]], removeAngles = ArrayPad[#, {{0, 0}, {0, -1}}] &, splitLines = Function[lines, Cases[Partition[spans, 2, 1], {start_, end_} :> lines[[ (start + 1) ;; end ]]]]}, (* execute commands. *) (* note that duplicate points created by left/right are not removed *) FoldList[Replace, {startx, starty, starta Degree}, filteredCommands] // removeAngles // splitLines] ]; (* executes LOGO commands within the context of the given L-system *) geometry[system_, iterations_] := Block[{ i = iterations, (* set a default offset if one isn't defined *) offset = (offset /. system) /. (offset -> {0., 0.})}, Hold[LOGO[LSystem[i, axiom, rules] /. conversions, Append[offset, orientation]]] /. system // ReleaseHold ]; (* generates the thumbnail for the given L-system *) thumbnail[system_] := Tooltip[ Graphics[Line /@ geometry[system, (thumbIterations /. system)], ImagePadding -> thumbPadding, ImageSize -> thumbSize], (name /. system), TooltipDelay -> .3]; (* these are the structure definitions for the curves. the list replacement is very flexible since it uses Mathematica's symbolic transformations -- I have two different methods of scaling here as examples. a scaling option that I didn't implement is to use matrix transformations *) curves = { { name -> "L\[EAcute]vy C Curve", orientation -> 0., axiom -> {forward[1]}, (* scaling method 1. scale within the rules of the L-system itself *) rules -> { forward[x_] -> {R, forward[Cos[45. Degree] x], L, L, forward[Cos[45. Degree] x], R}}, conversions -> { L -> left[45], R -> right[45]}, plotRange -> {{-.5, 1.5}, {-1, .25}}, thumbIterations -> 5, maxIters -> 13, maxShowNext -> 8 }, { name -> "Sierpinski Triangle", orientation -> 60. Mod[i, 2], axiom -> {A}, rules -> { A -> {B, R, A, R, B}, B -> {A, L, B, L, A}}, (* scaling method 2. scale "globally" after iteration *) conversions -> { A -> forward[2.^(-i)], B -> forward[2.^(-i)], L -> left[60], R -> right[60]}, plotRange -> {{0, 1}, {-.1, 1}}, thumbIterations -> 3, maxIters -> 9, maxShowNext -> 6 }, { name -> "Hilbert Curve", orientation -> 180., axiom -> {A}, rules -> { A -> {L, B, F, R, A, F, A, R, F, B, L}, B -> {R, A, F, L, B, F, B, L, F, A, R}}, conversions -> { F -> forward[2.^(-i)], L -> left[90], R -> right[90]}, plotRange -> {{-1, .01}, {-1.01, .01}}, thumbIterations -> 3, offset -> {-2.^(-i-1), -2.^(-i-1) }, maxIters -> 7, minIters -> 1, maxShowNext -> 5 }, { name -> "Heighway Dragon Curve", orientation -> 45. i, axiom -> {F, X}, rules -> { X -> {X, R, Y, F, R}, Y -> {L, F, X, L, Y}}, conversions -> { F -> forward[Sqrt[2.]^(-i)], R -> right[90], L -> left[90]}, plotRange -> {{-.4, 1.22}, {-.5, .8}}, thumbIterations -> 5, maxIters -> 13, maxShowNext -> 8 }, { name -> "Pinwheel Embroidery", orientation -> 45., axiom -> {X, push, L, X, R, R, X, pop, R, X, L, L, X, R, F}, rules -> { F -> {F, push, L, X, R, R, X, pop, R, X, L, L, X, R, F}, X -> {F, push, L, F, R, R, R, F, pop, R, F, L, L, F, R, F}}, conversions -> { F -> forward[1], R -> right[45], L -> left[45]}, plotRange -> Automatic, thumbIterations -> 2, maxIters -> 4, maxShowNext -> -1 }, { name -> "Koch Snowflake", orientation -> 0., axiom -> {F, right[120], F, right[120], F}, rules -> { F -> {F, left[60], F, right[120], F, left[60], F}}, conversions -> { F -> forward[3.^(-i)]}, plotRange -> {{-.1, 1.1}, {-.92, .33}}, thumbIterations -> 2, maxIters -> 5, maxShowNext -> 3 }, { name -> "Ces\[AGrave]ro Curve", orientation -> 0., axiom -> {F}, rules -> { F -> {F, L, F, R, R, F, L, F}}, conversions -> { F -> forward[(2 + 2 Cos[85. Degree])^(-i)], R -> right[85], L -> left[85]}, plotRange -> {{0, 1}, {-.1, .5}}, thumbIterations -> 2, maxIters -> 7, maxShowNext -> 5 }, (* empirically find magnitude/rotation transform for Gosper curve since it's not immediately straightforward *) Module[{gosper, abs, arg}, gosper[abs_, arg_, baseAngle_] := { name -> "Gosper Curve", orientation -> baseAngle + arg Degree^(-1) i, axiom -> {F, X}, rules -> { X -> {X, R, Y, F, R, R, Y, F, L, F, X, L, L, F, X, F, X, L, Y, F, R}, Y -> {L, F, X, R, Y, F, Y, F, R, R, Y, F, R, F, X, L, L, F, X, L, Y}}, conversions -> { F -> forward[abs^(-i)], R -> right[60], L -> left[60]}, plotRange -> {{-.4, 1}, {-.2, 1.2}}, thumbIterations -> 2, maxIters -> 5, maxShowNext -> 3 }; {abs, arg} = Complex @@ (geometry[gosper[1., 0., 0.], 1] // Last // Last) (* last point *) // {# // Abs, # // Arg} &; gosper[abs, -arg, 90.]], { name -> "Penrose Tiling", orientation -> If[i > 6, 0., {36., 0., 0., 36., 36.}[[i]]], axiom -> {SV, 7, RS, 2R, SV, 7, RS, 2R, SV, 7, RS, 2R, SV, 7, RS, 2R, SV, 7, RS}, rules -> { 6 -> {8, 1, 2R, 9, 1, 4L, 7, 1, SV, L, 8, 1, 4L, 6, 1, RS, 2R}, 7 -> {R, 8, 1, 2L, 9, 1, SV, 3L, 6, 1, 2L, 7, 1, RS, R}, 8 -> {L, 6, 1, 2R, 7, 1, SV, 3R, 8, 1, 2R, 9, 1, RS, L}, 9 -> {2L, 8, 1, 4R, 6, 1, SV, R, 9, 1, 4R, 7, 1, RS, 2L, 7, 1}, 1 -> {}}, conversions -> { 1 -> forward[1], (x_ : 1) L -> left[36 x], (x_ : 1) R -> right[36 x], SV -> push, RS -> pop}, plotRange -> Automatic, customStyle -> {JoinForm["Round"]}, thumbIterations -> 1, maxIters -> 5, minIters -> 1, maxShowNext -> 3 }, { name -> "Plant", orientation -> 90., axiom -> {F}, rules -> { F -> {F, push, L, F, F, pop, F, push, R, F, F, pop, F}}, conversions -> { F -> forward[3.^(-i)], L -> left[25], R -> right[25]}, plotRange -> {{-.4, .48}, {-.01, 1.36}}, thumbIterations -> 2, maxIters -> 4, maxShowNext -> 3 } }; (* the choices that will populate the SetterBar *) choices = (# -> thumbnail[#]) & /@ curves; Manipulate[ maxIterations = (maxIters /. system); (* readjust slider max *) iterations = Min[iterations, (maxIters /. system)]; (* main Manipulate output *) Tooltip[ Show[ (* next iteration *) If[showNext && (iterations <= (maxShowNext /. system)), Graphics[Join[ Block[{i = iterations + 1}, nextStyle], {Thickness[lineThickness/2]}, Line /@ geometry[system, iterations + 1]]], {}], (* current iteration *) Graphics[Join[ {color, Thickness[lineThickness]}, (customStyle /. system) /. (customStyle -> {}), Line /@ geometry[system, iterations]]], PlotRange -> (plotRange /. system), ImageSize -> imageSize], (* tooltip content *) Framed[Column[{ (name /. system) <> " L-system at " <> ToString[iterations] <> " iteration" <> If[iterations =!= 1, "s", ""], Null, ToString[(name /. system)] <> " Construction:", Null, Grid[{{"Axiom:", (axiom /. system)}}], Null, Grid[{{"Transformation rules:", MatrixForm[{rules /. system}//Transpose]}}], Null, Grid[{{"Definitions:", MatrixForm[{conversions /. system} // Transpose], If[Count[conversions /. system, i, Infinity] > 0, "With i = the current iteration"]}}]}], ImageMargins -> 3, FrameMargins -> 0, FrameStyle -> None], TooltipDelay -> .6], OpenerView[{"Style", Column[{ Control[{{color, Black, "line color"}, ColorSlider}], Control[{{lineThickness, 0.005, "line thickness"}, 0, .02, .005}], Control[{{showNext, True, "show next iteration"}, {True, False}}]}]}], {{system, curves[[2]], "L-system"}, choices, ControlType -> SetterBar}, {{iterations, 1, "iterations"}, 0, Dynamic[maxIterations], 1, Appearance -> "Labeled", (* disable animation, since it plays poorly with Dynamic[maxIterations] *) ContinuousAction -> False, ControlType -> Slider}, SynchronousUpdating -> False]
This is however basically the first Mathematica program I wrote. For a slightly different, not necessarily better approach, see my 3D-capable l-system 3D 1, and some of the images I produced with it. For a soup-to-nuts L-system in a minimal piece of code, see l-system.
