oftenpaper.net

toRiemann = Compile[{{pts, _Real, 2}}, Module[{k},
    Map[(k = 2/(1 + #.#); {k #[[1]], k #[[2]], 1 - k}) &, pts]]];

invertRiemann[pts_] := {#1, #2, -#3} & @@@ pts;
(*fromRiemann[pts_]:=(-1/(#3-1)) {#1,#2,0}&@@@pts;*)

shuttle = With[{shuttleGC = ExampleData[{"Geometry3D", "SpaceShuttle"}, "GraphicsComplex"]},
   Translate[#, {0, 0, 100}] &@
    {EdgeForm[None], Lighting -> "Neutral",
     Append[shuttleGC, VertexColors -> RandomReal[.65 + {0, 1}, Length[shuttleGC[[1]]]]^2]}];

cow = Translate[#, {0, 0, 1.2}] &@
   {EdgeForm[None],(*Opacity[.999],*)Texture[Graphics[Disk[]]], Lighting -> "Neutral",
    Append[ExampleData[{"Geometry3D", "Cow"}, "GraphicsComplex"],
     VertexTextureCoordinates -> 1/500 ExampleData[{"Geometry3D", "Cow"}, "PolygonData"]]};

allSettings = {"sphere", "cow", "original", "riemann", "inverse", "shuttle"};

bookmarks = {
   "Random" :> (
     With[{R := RandomReal[]},
      color = RGBColor[R, R, R];
      inflection = RandomChoice[{1, -1}];
      effect = .25*R^8; thickness = 10*R^8;
      spirality = R^3;
      If[spirality < .035, spirality = 0];
      x = 12 R; y = 2 R];

     Module[{weights = If[x > 3, {.1, .03, .87}, {.1, .07, .83}]},
      \[Zeta] = RandomChoice[{-1, 1}]*
        RandomChoice[weights -> {
           RandomReal[{0, 7.5}],
           RandomChoice[{0, .5, .5}],
           Round[RandomReal[{1, 7.5}], .5]}]]),

   "Rose" :> {color = Red, effect = 0, inflection = -1, x = 0, y = 1.1343, spirality = 0, \[Zeta] = 3},
   "Glyph" :> {color = Black, effect = 0.198, inflection = 1, x = 5.2, y = 0, spirality = 0, \[Zeta] = 2},
   "Mass Atomic" :> { effect = 0, inflection = -1, x = 5.84, y = 0.412, spirality = 0, \[Zeta] = -4.2504},
   "Jello" :> {color = Red, effect = 0, inflection = -1, x = 12, y = 0.846, spirality = 1, \[Zeta] = -1},
   "Grim" :> {thickness = 3.35, color = Black, effect = 0.0675, inflection = 1, x = 8, y = 0.296, spirality = 1, \[Zeta] = -1},
   "Angelwings" :> {color = RGBColor[.07694, .39046, 1], effect = 0, inflection = 1, spirality = 1, x = 12, y = 0, \[Zeta] = -5.4947},
   "Rollers" :> {color = Black, effect = 0, inflection = -1, spiral3ity = 0, x = 5.5, y = .1, \[Zeta] = -0.984032039033508},
   "Lifespark" :> {color = RGBColor[.1026, .9878, .0201], effect = 0, inflection = 1, spirality = .0995, x = 3.2757, y = .2002, \[Zeta] = -5.5}};       

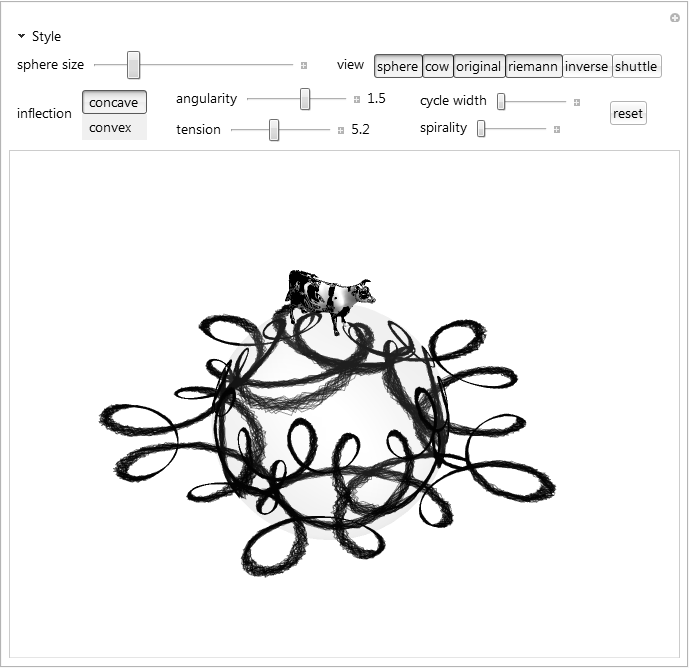
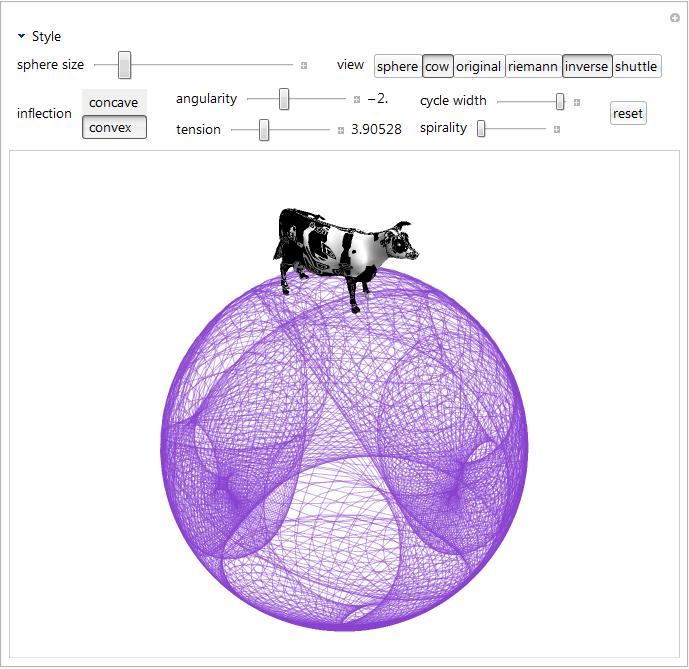
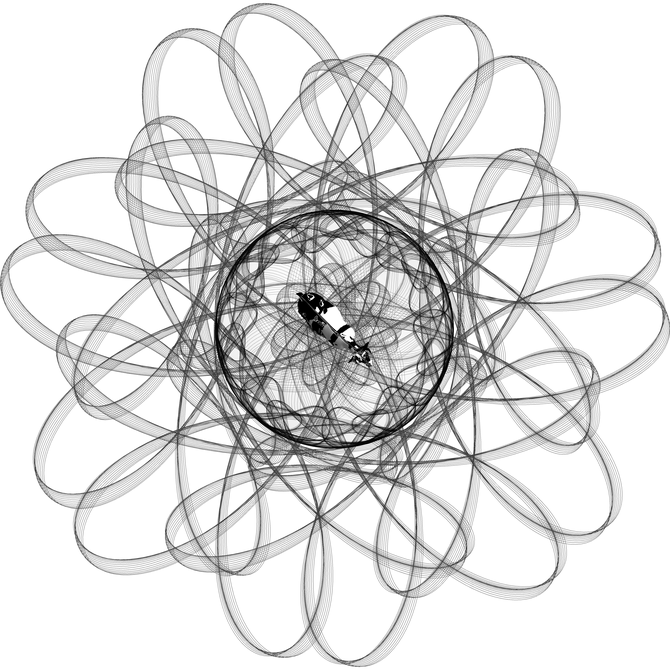
With[{
  colorC = Control[{{color, Black, "line color"}, ColorSlider}],
  backgroundC = Control[{{background, White}, ColorSlider}],
  thicknessC = Control[{{thickness, .001, "line thickness"}, .001, 10, Appearance -> "Labeled", ImageSize -> Small}],
  effectC = Control[{{effect, 0., "charcoal effect"}, 0, .25, Appearance -> "Labeled", ImageSize -> Small}],
  inflectionC = Control[{{inflection, 1}, {1 -> " concave ", -1 -> " convex "}, Appearance -> "Vertical"}],
  angularityC = Control[{{\[Zeta], 2., "angularity"}, -7.5, 7.5, .5, Appearance -> "Labeled", ImageSize -> Small}],
  tensionC = Control[{{x, 8., "tension"}, 0, 12, Appearance -> "Labeled", ImageSize -> Small}],
  yC = Control[{{y, 2., "cycle width"}, 0, 2, ImageSize -> Tiny}],
  spiralityC = Control[{{spirality, 0.}, 0, 1, ImageSize -> Tiny}],
  scaleC = Control[{{scale, 3.157, "sphere size"}, .00001, 15, ImageSize -> Medium}],
  settingsC = Control[{{settings, Take[allSettings, 4], "view"}, allSettings, ControlType -> TogglerBar}],
  opacityC = Control[{{opacity, .43}, 0, 1, Appearance -> "Labeled", ImageSize -> Small}],
  resetC = DynamicWrapper[
    Tooltip[Setter[Dynamic[reset], "reset"], "reset perspective", TooltipDelay -> .3],
    If[reset === "reset", (reset = False; vp = {1.3, -2.4, 2}; vv = {0, 0, 1}; {va, vc} = Automatic {1, 1})]]},

 With[{
   controls = Sequence[
     OpenerView[{"Style",
       Column[{
         Row[{
           Column[{backgroundC, colorC}, Alignment -> Right],
           Column[{effectC, thicknessC, opacityC}, Alignment -> Right]},
          Spacer[30]],
         Style[\[HorizontalLine], Lighter[LightGray]]}, Spacings -> 0]}],
     Row[{scaleC, Spacer[30], settingsC}],
     Row[{inflectionC, Spacer[30],
       Column[{angularityC, tensionC}],
       Column[{yC, spiralityC}], Spacer[30], resetC}]],

   storedVars = Sequence @@ ({{#, Automatic}, ControlType -> None} & /@ {vp, vv, va, vc}),
   dynamicView = Sequence[
     ViewPoint -> Dynamic[vp], ViewVertical -> Dynamic[vv],
     ViewAngle -> Dynamic[va], ViewCenter -> Dynamic[vc]]},

  (# /. switch[a_, b_] :> (*macro*)
       Unevaluated[Dynamic[If[MemberQ[settings, a], b, {}]]] &)@
   Manipulate[
    DynamicModule[{g, lines, riemannLines, invertedLines,
      \[Psi] = Round[Abs[FractionalPart[\[Zeta]]]*1., .25] /. {
         0. -> y, .5 -> y/2, .25 | .75 -> y/4}},

     g = ParametricPlot[
       1/(scale^1.4) (1. + spirality*(Log[\[Theta] + 1.] - 1.))*
        {\[Psi] Cos[\[Theta]] + x  Cos[64. \[Theta]] + (1 - effect*RandomReal[])*\[Zeta]* (Cos[512. \[Theta]] + Cos[64. \[Zeta] \[Theta]]),
         \[Psi] Sin[\[Theta]] - x Sin[64. \[Theta]] + (1 - effect*RandomReal[])* inflection*\[Zeta]* (Sin[512. \[Theta]] + Sin[64. \[Zeta] \[Theta]])}

       , {\[Theta], 0, 2 \[Pi]}, ImageSize -> {640, 480}, PerformanceGoal -> "Quality",
       Epilog -> {Gray, Thick, Circle[{0, 0}, 1]},
       PlotStyle -> Dynamic[{{color, Opacity[.43]}}], PlotRange -> Full,
       Background -> Dynamic[background], PlotPoints -> 270, Axes -> None];

     lines = Cases[g, Line[pts_] :> pts, Infinity];
     riemannLines = toRiemann /@ lines;
     invertedLines = invertRiemann /@ riemannLines;
     lines = Map[{##, 0} & @@@ # &, lines];

     ControlActive[g,
      Graphics3D[{
        switch[ "sphere", {Lighting -> "Neutral", Opacity[.1], Sphere[]}],
        switch["shuttle", shuttle], switch["cow", cow],
        Dynamic[color], Dynamic[Opacity[opacity]],
        Dynamic[AbsoluteThickness[thickness]],
        switch["original", Line /@ lines],
        switch["riemann", Line /@ riemannLines],
        switch["inverse", Line /@ invertedLines]}, Boxed -> False,
       dynamicView, Background -> Dynamic[background],
       ImageSize -> {640, 480}]]]

    , controls,
    storedVars,
    {{reset, "reset"}, ControlType -> None},

    Bookmarks -> bookmarks, Alignment -> Center]]]